Seine operation

Class modelling the operation of danish seining.

Collaboration diagram for Seine operation:

Author

Karl-Johan Reite

Date

23.04.2010 KJR: Initial version.

This class controls the operation of danish seining, by giving control input to the vessel, as well as controlling the CSeineConnector object, which is the buoy used in the operation. It controls the warp lengths, if the buoy is set and in which position, the speed of the vessel, and the desired heading of the vessel. Its input parameters define the operation.

Input parameters:

AttractorNameNet

Name of the attractor acting on the net nodes.

AttractorNameWarps

Name of the attractor acting on the warp nodes.

InitialSpeed

The speed of the vessel before the operation is started.

SetSpeed

The speed of the vessel during deployment of net and warps.

TowSpeed

The speed of the vessel during towing of the net, before hauling is started.

HaulSpeed

The speed of the vessel during hauling of the net.

FinishedSpeed

The speed of the vessel after the operation is finished.

WinchHaulSpeed

The winch speed during hauling (m/s).

InitialHeading

The vessel heading before deployment starts.

TowHeading

The vessel heading during towing.

SpreadAngle

The angle between the two warps.

WarpLength

The lenth of the warps.

TowTime

The time to tow the net after hauling.

AddedTrackLength

An addition to the track length to make the net deploy at the correct time. This corrects for the length of the net, as well as the distance the first warp is towed through the water until the net is set.

Definition of operation and parameters

Definition of seine operation.

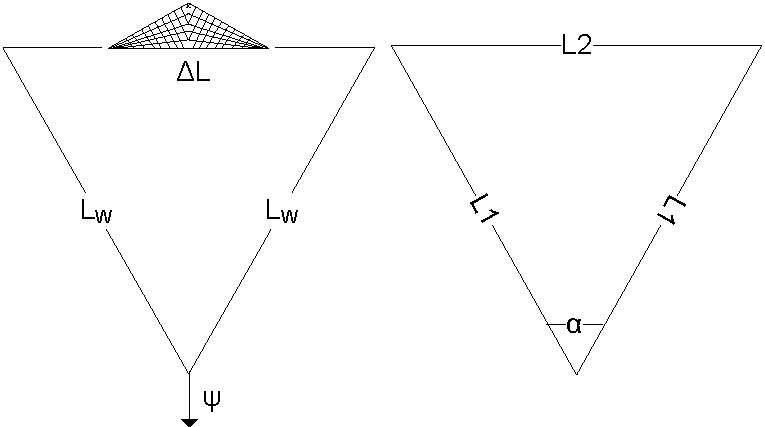
The image shows how the trajectory of the vessel is defined. Basically, the total length of the trajectory, \(L\), is found as

\[L = L1 + L2 + L1\]

, where L1 and L2 are the sides of the equilateral triangle that forms the path of the vessel.

Further we have that:

\[ L = L_1 + L_2 + L_1 \]

\[ L = 2L_W + \Delta L \]

\[ 2 sin \frac{\alpha}{2} = \frac{\frac{L_2}{2}}{L_1} \]

Combining these equations, we get:

\[ L_2 = \frac{L}{1+\frac{1}{2 sin \frac{\alpha}{2}}} \]

\[ L_1 = \frac{L_2}{4 sin \frac{\alpha}{2}} = \frac{L - L_2}{2}\]

Using these equations, the trajectory of the vessel is found based on the input ( \( L_W, \Delta L, \psi, \alpha \) ).

The calculations of vessel heading are trivial and not explained in detail, but the headings are found based on the specified final heading and spread angle.

This SimObject is referred to as Seine/Operation